链式表示
链式表示
顺序表的插入、删除操作需要移动大量元素,影响了运行效率(虽然时间复杂度为O(1)的情况也存在)。
链式存储线性表时,不需要使用连续的存储单元,不要求逻辑上相邻的两个元素在物理位置上也相邻
理解“链”的含义,链条--->捆绑、指向------>指针
链式存储线性表时,对线性表的插入、删除元素是不需要移动元素的,只是需要修改指针
单链表
基本概念
线性表的链式存储称作单链表,通过一组任意的存储单元来存储线性表中的数据元素。
每个链表结点(node)除了存放元素自身的信息外,还需要存放一个指向其后继结点的指针。目的是:通过指针建立起链表元素之间的线性关系
单链表中结点类型的描述:
// 单链表结点类型定义
typeof struct LNode{
ElemType data; // 数据域
struct LNode *next; // 指针域
}LNode , *LinkList;单链表可以解决顺序表需要大量连续存储空间的缺点,但是单链表在数据域的基础上附加了指针域,存在浪费存储空间的缺点;
单链表的元素是离散地分布在存储空间中的,因此单链表是非随机存取的存储结构,不能直接找到表中特定的结点,需要从头开始遍历、一次查找;
通常,头指针用来标识一个单链表。头指针指向NULL时,标识单链表为空。
头结点
为了操作上的方便,在单链表第一个结点之前附加一个结点,叫做头结点。
- 头结点的数据域可以不存任何信息、也可以记录表长等基础信息
- 头结点的指针域指向线性表的第一个元素结点;
不论单链表是否带头结点(可选),头指针始终指向链表的第一个结点。
头结点是带头结点的链表中的第一个结点【重要】
- 头结点的数据域可以不存任何信息、也可以记录表长等基础信息
- 头结点的指针域指向线性表的第一个元素结点;
头结点的优点:
- 因为开始结点的位置被存放在头结点的指针域中,所以在链表的第一个位置上的操作和在表的其他位置上的操作一致,不需要进行特殊处理;
- 无论链表是否为空,头指针始终是指向头结点的头结点的非空指针【空表中,往往就只有头结点,此时头结点的指针域为空,可以有效避免头指针空指针异常问题】-----> 头结点的引入,很好的统一了空表和非空表的操作;
头插法
从空表开始,生成新的结点,将读取的数据存放在新结点的数据域中,将新结点插入到当前链表的表头【头结点之后】
/*
* @Description: 单链表头插法创建
* @Version: Beta1.0
* @Author: 微信公众号:储凡
* @Date: 2020-03-04 23:38:04
* @LastEditors: 微信公众号:储凡
* @LastEditTime: 2020-03-04 23:39:16
*/
LinkList CreateListWithStartNode(LinkList &L){
LNode *s;
int x;
L=(LinkList)malloc(sizeof(LNode)); // 创建头结点L
L->next=NULL; // 初始化空链表
// 控制台输入值
scanf("%d",&x);
// 输入9999 表示结束
while(x!==9999){
// 开辟新结点存储空间
s=(LNode*)malloc(sizeof(LNode));
// 结点数据域赋值
s->data=x;
// 修改指针,新结点插入表中【注意:L->next为头结点的指针域】
s->next=L->next;
L->next=s;
scanf("%d",&x);
}
// 返回单链表
return L;
}特点:
- 读入数据的顺序与生成的链表中的元素顺序是相反的【结合队列先进先出思考】
- 每个结点插入的时间复杂度为O(1),单链表长度为n时,头插法的时间复杂度为O(n)【结合算法中的while循环,可以很明确看出时间复杂度】
尾插法
头插法建立的单链表,链表中结点的次序和输入数据的顺序不一致【相反】,尾插法则很好的避免了这个问题;
新结点插入到当前链表的表尾上,必须增加一个尾指针r,始终指向当前链表的尾结点;
/*
* @Description: 单链表尾插法创建
* @Version: Beta1.0
* @Author: 微信公众号:储凡
* @Date: 2020-03-04 23:38:04
* @LastEditors: 微信公众号:储凡
* @LastEditTime: 2020-03-04 23:39:16
*/
LinkList CreateListWithEndNode(LinkList &L){
int x; // 输入结点值
L=(LinkList)malloc(sizeof(LNode));
LNode *s; // 新结点s
LNode *r=L; // r为尾指针
// 控制台输入值
scanf("%d",&x);
while(x!==9999){
// 开辟新结点存储空间
s=(LNode *)malloc(sizeof(LNode));
// 新结点s的数据域赋值为x
s->data=x;
// 单链表L的尾指针指向新的结点s
r->next=s;
// 指针r指向新的表尾结点
r=s;
scanf("%d",&x);
}
// 表尾指针置空【重要】
r->next=NULL;
// 返回单链表
return L;
}特点:
- 读入数据的顺序与生成的链表中的元素顺序完全一致
- 每个结点插入的时间复杂度为O(1),单链表长度为n时,尾巴插法的时间复杂度为O(n)【结合算法中的while循环,可以很明确看出时间复杂度】
- 相比头插法附设了一个指向表尾结点的指针,但时间复杂度与头插法相同
按序号查找
在单链表中从第一个结点出发,顺指针next域逐个往下搜索、遍历,直到找出第i个结点为止,否则返回最后一个结点指针域NULL
/*
* @Description: 单链表按序号查找
* @Version: Beta1.0
* @Author: 微信公众号:储凡
* @Date: 2020-03-04 23:38:04
* @LastEditors: 微信公众号:储凡
* @LastEditTime: 2020-03-04 23:39:16
*/
LNode *GetElem(LinkList L,int i){
int j=1; // 查询计数,初始为1
LNode *p=L->next; // 单链表头结点指针赋值给指针p
// 第0个元素,则指向头结点,返回头结点
if(i==0){
// 头结点包含数据域和指针域
return L;
}
// 不等于0,却小于1,则i为负数无效,直接返回NULL,查询结果空;
if(i<1){
return NULL;
}
// p存在且计数没有走到初始i的位置
while(p&&j<i){
// 指针后移
p=p->next;
// 计数标记+1
j++;
}
// 注意: 当p不存在时, 跳出循环,p=NULL; 当p存在但是j大于等于i,跳出循环,返回查找的结果,返回p
// 从跳出循环上来分析,p要么存在即:找到的结点元素,要么为空即NULL
// 跳出循环,返回第i个结点的指针
return p;
}需要遍历(扫描)单链表,时间复杂度为:O(n)
按值查找
从单链表的第一个结点开始,从前往后依次比较表中个结点数据域的值,等于给定值e,则返回该结点的指针;若整个单链表【遍历完】中没有数据域值为e的结点,则返回NULL;
LNode *LocateElem(LinkList L,ElemType e){
// 指针【哨兵】
LNode *p=L->next;
// 从第1个结点开始查找数据域(data)为e的结点
while(p!=NULL&&p->data!=e){
// 无法匹配,指针后移
p=p->next;
}
// 注意:p为NULL的时候,说明单链表已经遍历的尾结点了,跳出循环,没有找到目标结点;
// 查找到第1个匹配的结点,跳出循环,返回结点指针
return p;
//
}链表遍历无法匹配,会返回NULL,因为在尾结点无法匹配的时候,直接返回尾结点指针域
需要遍历(扫描)单链表,时间复杂度为:O(n)
结点插入
单链表中,将值为x的新结点插入到单链表的第i个位置上
- 第一步: 检查插入位置的合法性;
- 第二步: 找到待插入位置的前驱结点,即第(i-1)个结点;
- 第三部: 在前驱结点后插入新结点;
// 循环遍历,时间复杂度O(n)
p=GetElem(L,i-1);
// 移动指针,时间复杂度O(1)
s->next=p->next;
p->next=s;结合上面的代码可以看出,将元素x插入到单链表L的第i个元素上,必须先找到单链表L的i个结点的前驱结点,即(i-1)的位置,需要采用GetElem()函数,按照序号查找;
如果返回的前驱结点不为空,则说明插入的位置i合法,否则位置非法,插入失败;
找到前驱结点p后,最重要的是移动指针,将新的结点s的指针域指向结点p的指针域,也就是s的指针域指向元素p的后继结点,第i个结点元素
原来的(i-1)位置上的元素,也就是前驱结点p的指针域则必须指向新的结点元素;
上面的过程不能更换,避免后继指针不存在的问题
最后的最后,一定要注意将s的数据域赋值x
插入结点的时间复杂度集中在查找第(i-1)个元素,时间复杂度为O(n);如果在给定结点的后面插入新结点,只需要执行p->next=s操作,时间复杂度为O(1)
前插操作
在某结点的前面插入一个新的结点
对结点的前插操作都可以转化为后插操作,前提:需要从单链表的头结点开始顺序查找到其前驱结点;时间复杂度为O(n)。
后插操作
在某结点的后面插入一个新的结点,单链表插入算法中,通常采用后插操作的
// 结点s插入到结点p的前面,修改指针域,顺序不能改变
s->next=p->next;
p->next=s;
// 经典的借助变量,进行值交换
temp=p->data;
p->data=s->data;
s->data=temp;上述借助临时变量temp来将结点s和结点p的数据域进行交换,需要开辟O(1)的空间复杂度,但是时间复杂度却从O(n)改变为O(1),典型的空间换时间策略
删除结点
将单链表L的第i个结点元素删除;
- 第一步: 先检查删除位置的合法性;
- 第二步: 查找表中的第(i-1)个结点,即被删结点的前驱结点;
- 第三步: 移动指针,删除结点元素;
// 获取删除位置结点元素的前驱结点
p=GetElem(L,i-1);
// 删除位置结点元素指针
q=p->next;
// 修改指针,将删除位置结点元素前驱结点的指针域指向其后继结点
p->next=q->next;
// 释放结点元素的内存控件
free(q)和插入算法一样,时间都消耗在查询前驱结点上,时间复杂度为:O(n)
删除单链表L中给点结点元素*p,通常是按值查找获取到p结点的前驱元素,再执行删除操作,这样很明显会导致时间复杂度为:O(n),主要都消耗在
按值查找上
这里可以利用p结点的后继结点将p结点删除
- 第一步:申请结点q,使其只想p结点的后继结点;
- 第二步:将p结点的数据域值换成其后继结点的数据域;【注意,交换没什么意义,最终p的后继结点会删除、释放】
- 第三步:p的指针域指向q的指针域,q结点从链中“断开”
- 第四步:释放q的内存空间
// 存放p的后继结点指针
q=p->next;
// 结点p的后继结点元素赋值给结点p,避免后继结点的数据域丢失
p->data=p->next->data;
p->next=q->next;
// 此时q指向更换数据域后的p,即原来p的后继结点
free(q)相比按值查找前驱结点来删除给定的结点p,利用后继结点来删除的时间复杂度更小,为:O(1)
计算表长
计算单链表中数据结点(不含头结点)的个数
算法思路:从第一个结点开始顺序依次访问表中的每一个结点,为此需要设置一个计数器变量,每访问一个结点,计算器加1,直到访问到空结点为止。
算法时间复杂度:O(n)
单链表的长度是不包括头结点的,不带头结点和带头结点的单链表在求表长操作上会略有不同。
不带头结点的单链表,当表为空时候,需要单独处理;
// 不带头结点的单链表L为空,判定条件是L=NULL。
if(L===NULL){
// 链表为空,表长为0
return 0;
}
// 带头结点的单链表L为空,判空条件:L->next=NULL;
if(L->next===NULL){
// 链表为空,不包含头结点,表长为0
return 0;
}双链表
从单链表的结构上来看
- 访问特定结点的前驱结点需要遍历整个单链表,移动指针,时间复杂度为:O(n)
- 访问特定结点的后继结点只需要移动一次指针,时间复杂度为:O(1)
双链表的引入,很好的解决单链表访问前驱结点时间消耗大的问题。
双链表结点由三部分组成:
数据域存放数据信息prior指针域指向结点的前驱结点next指针域指向结点的后继结点
// 双链表结点类型
typedef struct DNode{
ElemType data; // 结点的数据域
struct DNode *prior; // 结点的前驱指针
struct DNode *next; // 结点的后继指针
}DNode, *DlinkList;基本特点
- 双链表仅仅在单链表的结点中增加了一个指向结点前驱的
prior指针; 按值查找、按序号查找在单链表和双链表上的操作是相同的。- 和单链表不同,
插入、删除操作除了修改next指针域,双链表还需要修改prior指针域,确保不断链,时间复杂度都为:O(1)
插入结点
在双链表中p所指的结点之后插入结点s
// 第一步
s->next=p->next;
// 第二步
p->next->prior=s;
// 第三步
s->prior=p;
// 第四步
p->next=s第一步和第二步必须再第四步之前,整体时间复杂度为:O(1)
删除结点
删除双链表中结点p的后继结点q
// 第一步
p->next=q->next;
// 第二步
q->next->prior=p;
// 第三步
free(q);第一步和第二步顺序可换,整体时间复杂度为:O(1)
循环链表
循环单链表
循环单链表是在单链表的基础上,将最后一个结点(尾结点)的指针由NULL改为指向头结点,形成环。【单链表----->循环单链表】
// 双链表结点类型
typedef struct DNode{
ElemType data; // 结点的数据域
struct DNode *prior; // 结点的前驱指针
struct DNode *next; // 结点的后继指针
}DNode, *DlinkList;判空条件
不是判断头结点的指针是否为空,而是需要判断是否等于头指针,表为空时,头结点的next指针域其实是指向自己;
特点
- 在循环单链表中,尾结点*p的next指针域指向链表L(即:头结点),形成了
闭环,不存在指针域为NULL的结点。 - 由于循环单链表是个
环,在任何位置上的插入、删除操作都是等价的,不需要去判断是否是表尾。当其中的结点的next指针指向自己,也就能判断表为空 - 单链表只能从头结点(表头结点)开始往后顺序遍历整个表,循环单链表可以从表中任意位置开始遍历整个链表,结点是等价的;
- 循环单链表可以抽象为时钟,形成的
环是有顺序的; - 频繁的
表头和表尾操作,可以对循环单链表设置尾指针,而不设置头指针,明确尾指针r后,头指针即为:r->next,减少头指针到尾指针间的遍历,时间复杂度:O(n)---->O(1)
循环双链表
循环双链表是在双链表的基础上,将尾结点的next指针指向头结点,将头结点的prior指针指向尾结点。【双链表----->循环双链表】
// 双链表结点类型
typedef struct DNode{
ElemType data; // 结点的数据域
struct DNode *prior; // 结点的前驱指针
struct DNode *next; // 结点的后继指针
}DNode, *DlinkList;判空条件
循环双链表为空时,头结点*p的prior指针和next指针都指向L,即同时满足:
- p->next=L
- p->prior=L
基本特点
- 从双向链表中的任意一个结点开始,都可以很方便地访问它的
前驱结点和后继结点。
静态链表
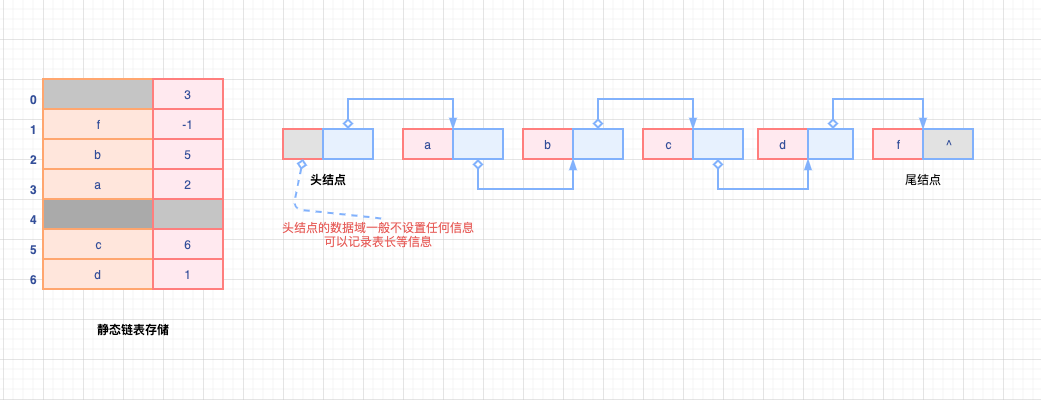
借助数组来描述线性表的链式存储结构,结点元素同样存在数据域
data和指针域next
注意: 和普通的链表的指针域不同的是,静态链表的指针是结点元素的相对地址(数组下标),也称为游标,建议结合高级语言中数组的概念来理解;
与顺序表一样,虽然静态链表属于链表,但是存储时需要预先分配一块连续的内存空间
静态链表结构类型:
// 定义静态链表的最大长度
# define MaxSize 50
typedef struct{
ElemType data; // 存储数据元素,数据域
int next; // 下个元素的相对地址,数组下标
}SLinkList[MaxSize];很显然,静态链表是通过数组游标来访问下一个结点元素,可以和指针域的相关概念结合理解;
- 静态链表以
next=-1作为结束的标志【尾结点】 - 和动态链表相同,插入、删除操作不需要移动元素,只需要修改指针;
- 总体来说,静态链表没有单链表使用方便,需要将整个链表存储在一块连续的内存空间中,内部的存储可以分散,通过指针构成
链的关系
更新日志
237b3-于77999-于93038-于483dc-于8a107-于564c3-于dc1d8-于fe3de-于898b8-于6a156-于7bd30-于aa128-于47c5b-于e2b22-于867b1-于ec5e2-于a6af0-于5666c-于
